João H de A Franco

The Traveling Rook July 11, 2017 - (0)
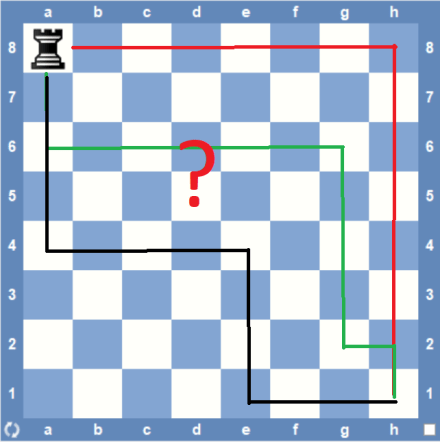
A rook is placed in the corner of a standard (8 x 8) chessboard. Every minute, it makes a legal move, where each move has the same probability of being chosen. What is the expected number of minutes for the rook to reach the opposite corner? This puzzle was proposed at the HMMT November 2015 competition […]
Who’s (really) the best chess player? September 20, 2014 - (0)
N-ary m-sequence generator in Python February 15, 2014 - (0)
HMAC-SHA-256 implementation in Python 3 June 11, 2013 - (0)
Validation of an AES-CFB implementation in Python 3 June 7, 2013 - (0)

Mobile Site | Full Site